Linear Regression
Trong bài viết này, mình sẽ giới thiệu về Linear Regression hay tên tiếng việt là “Hồi quy tuyến tính” (nghe sang phết). Đây là một trong những thuật toán cơ bản nhất của Machine Learning và là nền tản của các mô hình Deep Learning phức tạp hơn.
Một bài toán thực tế
Giả sử chúng ta đang làm một khảo sát số giờ học và điểm thi của các học sinh trong một lớp.
Sau khi đi hỏi một vài bạn trong lớp, ta có một bảng dữ liệu nhỏ như sau:
| Học sinh | Số giờ học | Điểm thi |
|---|---|---|
| 0 | 2 | 5 |
| 1 | 5 | 7 |
| 2 | 9 | 9.5 |
| 3 | 3 | 6 |
| 4 | 8 | 9 |
Để dễ hình dung hơn, hãy vẽ nó lên một biểu đồ, với trục hoành là Số giờ học và trục tung là Điểm thi. Mỗi cặp dữ liệu (giờ học, điểm) là một điểm trên biểu đồ.
Nhìn vào biểu đồ, bạn thấy gì không? Rõ ràng là có một xu hướng: học càng nhiều giờ thì điểm càng cao. Các điểm này trông có vẻ như đang nằm trên hoặc gần một đường thẳng nào đó.
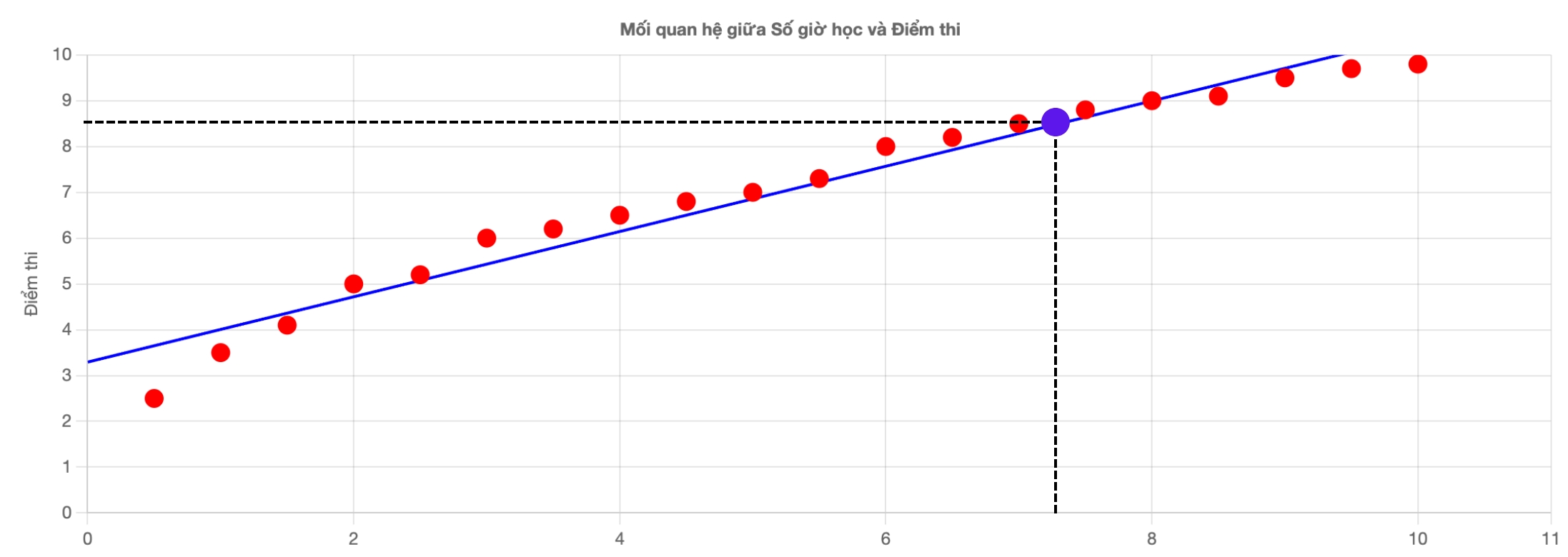
Bây giờ chúng ta sẽ tiếp tục thu thập thêm dữ liệu và vẽ thêm vào biểu đồ để có thể hình dung dễ hơn.
Bây giờ thì xu hướng đã quá rõ ràng! Các điểm dữ liệu dường như đang xếp thành một đường đi lên từ trái sang phải. Ta có thể rút ra một nhận xét quan trọng: Có một mối quan hệ đồng biến giữa thời gian học và điểm thi. Thời gian học càng tăng thì điểm thi có xu hướng càng cao.
Nhận xét trên rất hữu ích, nhưng sức mạnh thực sự của nó nằm ở khả năng dự đoán.
Bây giờ, bài toán thú vị hơn xuất hiện: Giả sử có bạn một bạn khác, không có trong bảng khảo sát, đã dành $6.25$ giờ để học bài. Dựa vào xu hướng mà chúng ta vừa phát hiện, liệu ta có thể dự đoán điểm của học sinh đó là bao nhiêu không?
Câu trả lời là có! Nhìn vào biểu đồ, ta có thể dự đoán kết quả của bạn đó sẽ là tầm khoảng $8$ đến $8.2$.
Giờ nếu ta đưa cho máy tính thì sao? Máy tính sẽ nhận vào:
- Danh sách
thời gian họcvàđiểmcác học sinh mà ta đã khảo sát. Thời gian họccủa một học sinh mà ta chưa khảo sát và hãy dự đoánđiểmcủa học sinh đó.
Máy tính giải quyết bài toán này như thế nào?
Chúng ta có thể “nhìn” vào biểu đồ và ước lượng, nhưng máy tính thì không. Nó cần một phương pháp rõ ràng, một công thức toán học cụ thể. Đây là lúc Linear Regression vào cuộc.
Giả sử thời gian học của một học sinh là $x$, và một hàm số “thần thánh” nào đó, ký hiệu là $f(x)$, có thể nhận vào $x$ rồi từ đó đưa lại cho ta một kết quả là $\hat{y}$, là điểm số dự đoán của học sinh đó. Ta có thể viết lại công thức dưới dạng như sau:
\[\begin{equation} \hat{y} = f(x) \label{eq:eq_1} \end{equation}\]Vì chúng ta nhận thấy xu hướng của dữ liệu trông giống một đường thẳng [Biểu đồ 2], nên hàm “thần thánh” $f(x)$ của chúng ta sẽ chính là phương trình của một đường thẳng. Ta sẽ viết lại công thức \eqref{eq:eq_1} thành dạng như sau:
\[\begin{equation} \hat{y} = f(x) = ax + b \label{eq:eq_2} \end{equation}\]Vậy, nhiệm vụ của máy tính giờ đây đã rõ ràng hơn: tìm một bộ giá trị của $(a;b)$ sao cho đường thẳng $\hat{y}=ax+b$ của chúng ta khớp với dữ liệu nhất có thể.
Nhưng câu hỏi quan trọng là: Làm thế nào để máy tính biết được một đường thẳng có “khớp” hay không? Giả sử bạn có hai đường thẳng, một tạo bởi $(a_1;b_1)$ và một bởi $(a_2;b_2)$, làm sao máy tính quyết định được đường nào “tốt” hơn? Vì vậy chúng ta cần một thước đo cụ thể, một con số để đánh giá “độ tốt” của mỗi đường thẳng.
Hàm Mất Mát (Loss Function) - Thước đo “độ tệ”
Trong Machine Learning, thay vì đo “độ tốt”, người ta thường đo lường “độ tệ” của một mô hình/đường thẳng. Con số này được gọi là sai số (error) hay mất mát (loss) của mô hình/đường thẳng đó với các điểm dữ liệu. Và ta có thể tính sai số đó bằng 2 công thức sau:
\[\begin{equation} \mathcal{L}(a,b) = \sum_{i = 1}^{N}{(y - y)^2} \begin{equation} \end{equation} \mathcal{L}(a,b) = \sum_{i = 1}^{N}{|y - y|} \end{equation}\]