Vector - Viên Gạch Nền Tảng Của Đại Số Tuyến Tính
Vector. Nghe quen đúng không?
Bạn có thể đã gặp nó đâu đó trong môn Toán, hay trong Vật Lý với mấy mũi tên chỉ lực rồi. Còn nếu chưa hoặc bạn đã quên thì bài viết này là dành cho bạn. À thực ra thì với các bạn còn nhớ về nó thì việc đọc bài viết này có thể giúp bạn hiểu thêm một vài khía cạnh khác của vector, mà có thể giáo viên trên trường đã không nói với bạn.
Trong lĩnh vực Khoa học Máy tính và đặc biệt là Machine Learning, vector không chỉ là những mũi tên. Nó là ngôn ngữ để chúng ta biểu diễn dữ liệu. Ta hãy cùng nhau mổ xẻ khái niệm này theo 2 góc nhìn chính, cũng như là 2 cách mà chúng ta sẽ dùng để biểu diễn vector.
Vector là một “mũi tên” trong không gian
Mô phỏng Gió và Vector
Hãy nhìn vào animation mô phỏng gió bạn đang thấy. Mũi tên màu xanh đó không chỉ là một hình vẽ, nó chính là một vector. Trong thế giới chúng ta, các đại lượng có hướng như lực, vận tốc, hay như trong ví dụ này là “gió”, đều được biểu diễn bằng vector.
Tại sao vậy? Vì để mô tả một cơn gió, chúng ta cần biết hai thông tin cốt lõi:
- Nó thổi theo hướng nào?
- Nó thổi mạnh như thế nào?
Hướng (Direction)
Hãy thử kéo thanh trượt “Hướng Gió”. Bạn sẽ thấy mũi tên xoay tròn. Khi nó chỉ sang phải, đó là gió thổi về hướng Đông. Khi nó chỉ lên trên, đó là gió thổi về hướng Bắc. Cái cách mà mũi tên “chỉ” vào một phía chính là hướng của vector. Mỗi giá trị từ 0° đến 360° tương ứng với một hướng duy nhất trong không gian.
Độ lớn (Magnitude)
Bây giờ, hãy kéo thanh trượt “Tốc Độ Gió”. Khi bạn tăng giá trị, mũi tên sẽ dài ra. Khi bạn giảm giá trị, nó ngắn lại. Độ dài của mũi tên này đại diện cho độ lớn (hay cường độ) của vector. Trong ví dụ này, độ lớn chính là tốc độ gió: một mũi tên dài thể hiện một cơn gió mạnh (ví dụ 100 km/h), trong khi một mũi tên ngắn chỉ là một làn gió nhẹ (ví dụ 10 km/h).
Như vậy, từ góc nhìn này, một vector đơn giản là một đối tượng gói gọn cả hai thông tin: Hướng và Độ Lớn.
Vị trí không quan trọng
Ở ví dụ bên trên, chúng ta vẽ mũi tên gió ở trung tâm để dễ quan sát. Nhưng hãy tưởng tượng, một cơn gió mạnh 100 km/h thổi về hướng Đông không chỉ tồn tại ở một điểm. Nó có thể đang thổi ở vị trí của bạn, và cũng đang thổi y hệt như vậy ở cách đó vài mét.
Miễn là hướng (hướng Đông) và độ lớn (100 km/h) không đổi, thì dù mũi tên đó được vẽ ở đâu, nó vẫn biểu diễn cùng một vector gió. Đây là một khái niệm cốt lõi: Vector được xác định bởi hướng và độ lớn, chứ không phải bởi vị trí bắt đầu của nó.
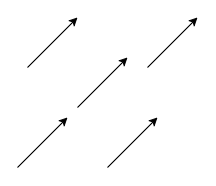Tất cả các mũi tên này đều biểu diễn cùng một vector vì chúng có cùng hướng và cùng độ dài.
Vector là một danh sách các con số
Góc nhìn về “mũi tên” có hướng và độ lớn rất trực quan, nhưng nó đặt ra một câu hỏi lớn: Làm thế nào để “bảo” một chiếc máy tính vẽ ra mũi tên đó? Máy tính không hiểu “hướng Đông-Bắc” hay “dài một chút”, nó chỉ làm việc với các con số.
Đây là lúc chúng ta cần một thứ để liên kết thế giới hình học và thế giới số. Cây cầu đó chính là hệ trục tọa độ.
Hãy tưởng tượng chúng ta đặt mũi tên vector vào một hệ trục tọa độ $Oxy$ quen thuộc. Để cho mọi thứ đơn giản và nhất quán, chúng ta luôn đặt gốc của mũi tên vào gốc tọa độ $(0, 0)$.
Khi đã làm vậy, toàn bộ vector giờ đây được xác định một cách duy nhất bởi một thứ: vị trí của đầu mũi tên. Và trong một hệ tọa độ, mọi vị trí đều có một “địa chỉ” rõ ràng.
Hãy thử tương tác với Animation dưới đây, chúng ta có thể biểu diễn một vector chỉ với tọa độ của đầu mũi tên của vector đó là điểm $(x,y)$.
Vector trong hệ tọa độ
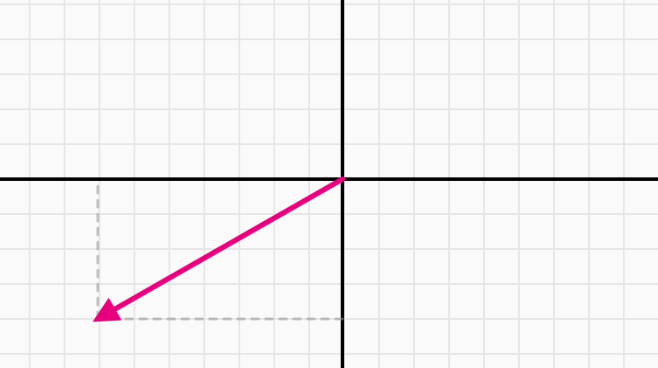
Đầu tiên, hãy dùng chuột kéo đầu mũi tên màu hồng đến một vị trí bất kỳ. Bạn sẽ thấy hai con số trong các ô input $v = [x, y]$ thay đổi theo ngay lập tức. Các con số này chính là tọa độ của đầu mũi tên. Đây là cách chúng ta “dịch” một đối tượng hình học (mũi tên) thành dữ liệu dạng số.
Tiếp theo, hãy thử làm ngược lại. Thay vì kéo mũi tên, bạn hãy thử nhập các con số vào ô input. Ví dụ, đổi $x=-5$ và $y=2$. Ngay lập tức, mũi tên sẽ tự điều chỉnh để đầu của nó chỉ vào đúng tọa độ $(−5,2)$.
Điều này cho thấy một sự tương ứng một-một (one-to-one correspondence):
- Mỗi mũi tên (bắt đầu từ gốc tọa độ) tương ứng với một cặp số duy nhất.
- Mỗi cặp số duy nhất tương ứng với một mũi tên duy nhất.
Điều này dẫn chúng ta đến góc nhìn thứ hai, và cũng là góc nhìn cốt lõi trong Khoa học Máy tính:
Trong đa phần các tài liệu, để phân biệt vector với các con số thông thường (scalars), người ta thường ký hiệu vector bằng một chữ cái in thường và in đậm (ví dụ $\textbf{v}$), hoặc có mũi tên ở trên (ví dụ $\vec{v}$).
Và đặc biệt trong Đại số Tuyến tính, quy ước chuẩn là viết vector dưới dạng vector cột (column vector):
\[\textbf{v} = \begin{bmatrix} 4 \\ 3 \\ \end{bmatrix}\]Con số ở trên ($4$) tương ứng với tọa độ trên trục $Ox$, và con số ở dưới ($3$) tương ứng với tọa độ trên trục $Oy$.
Tuy nhiên, khi lập trình, chúng ta thường biểu diễn nó như một mảng (array) hoặc danh sách (list): v = [4 3]. Trong văn bản, để tiết kiệm không gian, đôi khi người ta cũng viết theo hàng, nhưng chúng ta cần nhớ rằng về mặt toán học, nó thường được xem là một cột.
Một vector đơn giản là một cách để "đóng gói" dữ liệu thành một danh sách các con số có thứ tự, đại diện cho vector đó không gian.
Liên kết hai góc nhìn: Tính toán Độ lớn từ Tọa độ
Chúng ta đã nói vector có Hướng và Độ lớn. Khi biểu diễn vector dưới dạng số \(\begin{bmatrix}x \\ y \end{bmatrix}\), làm sao chúng ta tính được độ lớn (độ dài) của nó?
Nếu nhìn vào ví dụ này, bạn có thể nhận ra một tam giác vuông quen thuộc được tạo bởi vector và hình chiếu của nó lên các trục tọa độ.
Độ dài/Độ lớn của vector trong hệ tọa độ
Cạnh huyền của tam giác vuông này chính là độ dài/độ lớn $S$ của vector. Hai cạnh góc vuông có độ dài lần lượt là $x$ và $y$. Theo định lý Pythagoras quen thuộc:
\[\begin{equation} S^2 = x^2 + y^2 \\ S = \sqrt{x^2 + y^2} \end{equation}\]Độ lớn của vector $\textbf{v}$ thường được ký hiệu là $|\textbf{v}|$.
Ví dụ với vector \(\textbf{v} = \begin{bmatrix}4 \\ 3 \end{bmatrix}\), độ dài/độ lớn của nó sẽ là:
\[\|\textbf{v}\| = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5\]Vector trong không gian $N$ chiều
Thế giới của chúng ta không chỉ có 2 chiều (2D). Trong không gian 3D, chúng ta cần thêm một trục $Oz$. Một vector trong 3D sẽ trông như thế này:
\[\textbf{u} = \begin{bmatrix} 2 \\ 3 \\ 5 \end{bmatrix}\]Nó vẫn là một mũi tên, bắt đầu từ $(0,0,0)$ và kết thúc tại $(4,3,5)$ trong không gian ba chiều (animation).
Vector trong không gian 3D
Bây giờ, hãy tiến xa hơn. Điều gì sẽ xảy ra nếu chúng ta có một vector 4 chiều?
\[\textbf{u} = \begin{bmatrix} 1 \\ -2 \\ 4 \\ 0.5 \end{bmatrix}\]Bạn sẽ vẽ nó như thế nào? Thật khó để hình dung một không gian 4 chiều. Bộ não của chúng ta không được thiết kế để làm việc đó. Đây chính là lúc góc nhìn “danh sách các con số” tỏa sáng.
Mặc dù chúng ta không thể vẽ vector 4 chiều, chúng ta hoàn toàn có thể biểu diễn và tính toán với nó. Nó chỉ đơn giản là một danh sách gồm 4 con số. Khái niệm này mở rộng ra cho bất kỳ số nguyên $N$ nào. Một vector $N$ chiều là một danh sách gồm $N$ con số.
Vector trong Khoa học Máy tính và Machine Learning
Trong Machine Learning, chúng ta hiếm khi làm việc với vector 2D hay 3D. Chúng ta thường làm việc với vector hàng trăm, hàng nghìn, thậm chí hàng triệu chiều.
Tại sao? Vì Vector là ngôn ngữ chung để biểu diễn dữ liệu.
Quá trình chuyển đổi dữ liệu thực tế (hình ảnh, văn bản, âm thanh…) thành dạng vector được gọi là Vectorization.
Hãy xem xét một vài ví dụ:
Ví dụ 1: Dữ liệu thuộc tính (Tabular Data)
Giả sử bạn đang xây dựng một hệ thống dự đoán giá nhà. Bạn có thông tin về một căn nhà dựa trên các đặc trưng (features) sau:
- Diện tích: $120m^2$
- Số phòng ngủ: $3$
- Khoảng cách đến trung tâm: $5.5km$
- Năm xây dựng: $2010$
Căn nhà này có thể được biểu diễn bằng một vector 4 chiều (còn gọi là vector đặc trưng - feature vector):
\[\textbf{v}=\begin{bmatrix} 120 \\ 3 \\ 5.5 \\ 2010 \end{bmatrix}\]Ví dụ 2: Hình ảnh (Image Data)
Hãy tưởng tượng một bức ảnh trắng đen nhỏ kích thước $28\times 28$ pixels (giống như các ảnh chữ số viết tay trong bộ dữ liệu MNIST nổi tiếng). Bức ảnh này có tổng cộng $28 \times 28=784$ pixel.
Máy tính có thể “duỗi phẳng” (flatten) bức ảnh này thành một danh sách dài các giá trị cường độ sáng của từng pixel, xếp theo thứ tự.
\[\text{images} = \begin{bmatrix} p_1 \\ p_2 \\ p_3 \\ ... \\ p_{783} \\ p_{784} \end{bmatrix}\]Đây là một vector trong không gian 784 chiều!
Ví dụ 3: Văn bản (Text Data)
Trong xử lý ngôn ngữ tự nhiên (NLP), các từ hoặc câu cũng được chuyển đổi thành vector (gọi là embeddings). Ví dụ, từ “Vua” có thể được biểu diễn bằng một vector (giả sử 300 chiều) chứa các giá trị số học mô tả ý nghĩa của nó và mối quan hệ với các từ khác như “Nữ hoàng”, “Đàn ông”, “Phụ nữ”.